250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 파이썬
- sqldeveloper
- jupyternotebook
- pgadmin
- psycopg2
- 복구
- oracle
- GridSearchCV
- 연결
- TensorFlow
- cpu
- psql
- 도커이미지
- 머신러닝
- SQL
- 쿼리
- 리눅스
- postgre
- 교차검증
- docker
- LOG
- 도커
- Memory
- 시계열
- Linux
- Docker image
- GPU
- 오라클
- Python
- Jupyter
Archives
- Today
- Total
areum
[시계열 분석] ARIMA를 이용한 기온 예측 본문
728x90
ARIMA에 대한 간단한 설명
- ARIMA(AutoRegressive Integrated Moving Average)는 자기 회귀 모델(AR)과 이동 평균 모델(MA)과 데이터의 정상성을 확보하기 위한 차분(I)을 합친 모델
- ARIMA모델은 AR , I, MA의 차수를 정해야 하는데 이는 ARIMA(p, d, q)로 나타낸다.
- AR의 차수는 p, I의 차수는 d, MA의 차수는 q로 표시한다. ARIMA(1,1,0) 일 경우 AR(1)와 I(1)를 합친 모델이라는 의미이다.
* 월 별 평균기온 분석하여 예측하기
1. 기본 library를 불러온다. ( 아래는 제가 많이 쓰는 library들이라 매번 분석할 때마다 아래 코드는 실행하고 분석해요 ! )
import matplotlib.pyplot as plt #시각화를 위한 설치
import matplotlib.font_manager as fm # 한글 폰트
import matplotlib #시각화를 위한 설치
import os, warnings
import pandas as pd #구조 변경 및 결합을 하기 위한 설치
import seaborn as sns #시각화를 위한 설치
import plotly.express as px #시각화를 위한 설치
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', None) #모든 행을 다 보여주라는 명령
pd.set_option('display.max_columns', None) #모든 열을 다 보여주라는 명령
# 그래프에서 마이너스 폰트 깨지는 문제에 대한 대처
matplotlib.rcParams['axes.unicode_minus'] = False
## 한글 폰트 적용 ( 안하면 한글 깨짐 )
f_name = fm.FontProperties(fname="C:/Windows/Fonts/malgunbd.ttf").get_name()
plt.rc('font', family=f_name)2. 날씨 데이터 불러오고 정보 확인하기
- 공공데이터(air) - 1968년 ~ 2019년 날씨 데이터 추출 > train
- 공공데이터(air_2020) - 2020년 날씨 데이터 추출 > test
air= pd.read_csv('air.csv',encoding='ANSI')
air_2020= pd.read_csv('air_2020.csv',encoding='ANSI') #예측을 확인해볼 미래 데이터
air.info()
3. 평균 기온 그래프로 확인
air.plot()
plt.xlabel('일시')
plt.ylabel('평균기온')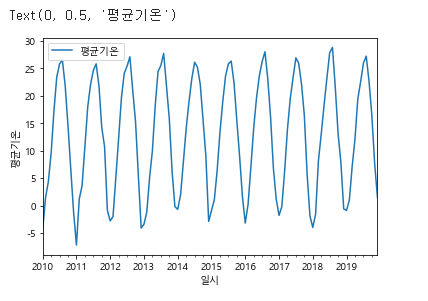
위 사진을 보면 일시별로 일정한 패턴이 존재함을 알 수 있습니다. 이는 비정상성 시계열의 특징을 가지고 있는 데이터입니다.
- 일상생활엔 비정상성 데이터들이 훨씬 더 많습니다. 따라서 정상성 데이터로 바꾼 뒤에 이 모델링을 할 수 있습니다.
- 비정상성을 정상성으로 바꾸는 방법
=> 바로 differencing(차분) 입니다.
4. ADF 검정
- 시계열 분석을 하기 위해서는 기본적으로 시계열이 정상성(stationary)이 있다는 가정을 만족해야 한다. 일반적으로 ADF(Augmented Dickey Fuller) Test 결과 p value 가 0.05 보다 작으면 정상성이 있다고 본다.
# AD-Fuller Test : 시계열의 정상성(stationary) 한지 확인
from statsmodels.tsa.stattools import adfuller
""" 차분 방법 """
air_diff =air - air.shift(1)
print(air)
y = air.dropna()
y1diff = air_diff.dropna()
result = adfuller(y)
print(f'원 데이터 ADF Statistic: {result[0]:.3f}')
print(f'원 데이터 p-value: {result[1]:.3f}')
result = adfuller(y1diff)
print(f'1차 차분 ADF Statistic: {result[0]:.3f}')
print(f'1차 차분 p-value: {result[1]:.3f}')
- 원 데이터의 p-value가 0.05넘으므로, 귀무가설을 기각하지 못한다. 해당 데이터는 정상성을 만족하지 못한다.
- 그렇기에, 1차 차분 진행 > 1차 차분을 한 것의 p-value가 0.05이하이므로 정상성을 보인다.
- 이로서 차분(d)의 차수는 1인 ARIMA(p, 1, q)의 모델 구축이 필요하다는 것을 알 수 있다.
이제 정상성을 만족하는 차분된 데이터로ARIMA 모형의 p와 q를 결정할 것입니다.
5. acf와 pacf 그래프를 그려 p,q를 구하는 2가지 방식
방법1. acf함수와 pacf함수 활용
plot_acf(air)
plot_pacf(air)
plt.show()
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
diff_1=air.diff(periods=1).iloc[1:]
diff_1.plot()
plot_acf(diff_1)
plot_pacf(diff_1)
plt.show()
- 위 그림으로는 p,q가 파악이 안된다고 생각하여 파라미터를 각각 대입하여 AIC가 가장 작은 값을 도출한다.
(파악이 안되는 이유 : 그래프를 해석할 때, lag(x좌표) = 인 지점은 읽지 않고 어느 지점부터 구간안에 들어가는지를 파악하면 되는데 PACF그래프를 보면 어디가 절단점인지 확실하게 알 수 없기 때문에 방법 2를 택하였습니다.)
방법2. 파라미터를 각각 대입하여 AIC가 가장 작은 값을 도출한다.
import itertools
p=d=q=range(0,5)
pdq=list(itertools.product(p,d,q))
pdqimport warnings
warnings.filterwarnings('ignore')
for param in pdq:
try:
model_arima=ARIMA(air.평균기온.values, order=param)
model_arima_fit=model_arima.fit()
print(param,model_arima_fit.aic)
except:
continue
- d가 1인 값들중 aic가 가장 낮은 (2,1,3)으로 결정
from statsmodels.tsa.arima_model import ARIMA
import statsmodels.api as sm
#(ar=2,차분=1, ma=3)파라미터로 arima모델을 학습
model=ARIMA(air['평균기온'], order=(2,1,3))
model_fit=model.fit(trend='nc',full_output=True,disp=1)
print(model_fit.summary())
- AIC (AKaike Information Criterion) : 데이터에 대한 모델의 상대적 품질
- 값이 낮을수록 모형 적합도가 높은것을 의미 합니다.
6. 예측값과 실제값의 비교
fig=model_fit.plot_predict()
residuals=pd.DataFrame(model_fit.resid)
residuals.plot()
7. 2020년도의 예측이 맞는지 확인
air_2020.index=air_2020['일시']
air_2020.set_index('일시',inplace=True)
air_2020_h=air_2020.head(12)
air_2020_h=air_2020.head(12)
forecast_data=model_fit.forecast(steps=12)
pred_y=forecast_data[0].tolist()
test_y=air_2020_h.평균기온.values
plt.plot(pred_y,color='red') #에측값
plt.plot(test_y,color='blue') #실제값
8. 예측성능 평가
from sklearn.metrics import mean_squared_error,r2_score
from math import sqrt
rmse=sqrt(mean_squared_error(pred_y,test_y))
print(rmse)36.334938142965676
'Programming > Machine Learning' 카테고리의 다른 글
| [ML] K-Means Clustering (K-평균 군집) (0) | 2023.03.17 |
|---|---|
| [ML] Association Rule Analysis (연관 규칙 분석) (0) | 2023.03.14 |
| [Machine Learning] GridSearchCV 하이퍼 파라미터 튜닝 (0) | 2022.12.01 |
| [Machine Learning] Random Forest (랜덤포레스트) (0) | 2022.11.30 |
| [Machine Learning] Multiple_regression (다중 회귀) (0) | 2022.07.19 |


